Hallo Ihr Lieben,
in diesem kleinen Beitrag wollte ich im Zusammenhang mit meiner Beitragsserie „Vom Zählen zur Mandelbrotmenge” einen alternativen Beweis zum traditionellen Beweis dafür präsentieren, dass die Wurzel aus 2 keine rationale Zahl sein kann. Auf diese Idee bin ich gekommen, weil ich beim Aufarbeiten des herkömmlichen Beweises – dem ich ja eigens einen kleinen Blogbeitrag gewidmet habe – festgestellt habe, dass man ihm zwar durchaus eine gewisse Eleganz nicht absprechen kann, er mich aber ganz am Ende trotzdem irgendwie in dem unbefriedigendem Gefühl zurücklässt, dass ich eigentlich immer noch nicht verstanden hat, was der wirkliche Grund dafür ist, dass die Wurzel aus 2 keine rationale Zahl sein kann.
Ich meine: ist ja schön und gut, dass man am Ende des traditionellen Beweises auf einen Widerspruch stößt, weil Zähler und Nenner eines angenommenen Bruchs für die Wurzel aus 2 einerseits teilerfrei sein sollen, während sie andererseits gleichzeitig die 2 als gemeinsamen Teiler haben müssten. Aber so wirklich klar wird mir deshalb nicht, was der eigentliche – sozusagen zahlenmechanische Grund dafür ist – dass es keinen Bruch mit ganzzahligem Zähler und Nenner geben kann, der mit sich selbst multipliziert 2 ergibt.
Also habe ich mir die Mühe gemacht, die Sache nochmals konstruktiv zu durchdenken – in der Hoffnung, dass ich einen echten Erkenntnisgewinn über den wahren Grund für die Irrationalität der Wurzel aus 2 verzeichnen kann. Nachstehend lest Ihr, was dabei herausgekommen ist:
Wir beginnen – im Moment noch genauso wie beim traditionellen Beweis – mit der Annahme, die Wurzel aus 2 sei eben doch eine rationale Zahl. Das heißt, wir nehmen an, es gäbe eine rationale Zahl, die mit sich selbst multipliziert 2 ergibt. Dann muss diese Zahl als Bruch aus zwei ganzen Zahlen a und b darstellbar sein (b ist natürlich ungleich 0 – sonst käme keine definierte Zahl heraus). Für diesen Bruch „a/b” müsste also gelten:
Nach den in meinem eigens dafür erstellten Blogbeitrag rekapitulierten Regeln für die Multiplikation zweier Brüche würde das der folgenden Gleichung entsprechen:
Bei genauer Betrachtung der Mechanik von Brüchen kommt man nicht an der Notwendigkeit vorbei, dass die 2 auf der rechten Seite der Gleichung (die ja eigentlich für den Bruch „2/1” steht) irgendwo als Teiler im Zähler a×a auf der linken Seite enthalten sein muss, damit sie letztlich aus (a×a)/(b×b) hervorgehen kann. Das muss so sein, weil der Nenner b×b keinen Beitrag zur Entstehung der 2 im Zähler des Ergebnisses rechts vom Gleichheitszeichen leisten kann, denn seine Teiler sorgen bestenfalls dafür, dass sie sich mit Teilern des Zählers a×a wegkürzen, die damit aus dem Zähler rechts vom Gleichheitszeichen „gelöscht” werden. Da nun aber rechts vom Gleichheitszeichen im Zähler gerade die 2 steht, muss sie aus dem Zähler a×a unseres Bruches gekommen sein:
Es gibt aber keine ganze Zahl, die man mit sich selbst multiplizieren kann, so dass 2 herauskommt (1×1 ist zu klein und 2×2 schon zu groß). Damit die 2 als Teiler in a×a vorkommen kann, muss sie daher also bereits als Teiler in a selbst enthalten gewesen sein (genauer gesagt, ein Teiler von a sein):
Dann allerdings liefert uns der Zähler a×a gleich zweimal unsere 2:
Da unser Ausgangsbruch aber nur die Zahl 2 und nicht etwa 2×2 zum Ergebnis haben soll, muss eine der beiden Zweien früher oder später wieder verschwinden. Das kann sie aber nur, wenn eine 2 als Teiler im Nenner b×b enthalten ist, mit der sie weggekürzt werden kann:
Da es – wie eben schon festgestellt – keine ganze Zahl gibt, die mit sich selbst multipliziert 2 ergibt, muss die aus b×b gelieferte 2 also irgendwie bereits in b selbst als Teiler enthalten sein (genauer gesagt, ein Teiler von b sein), so dass sie ebenfalls gleich zweimal unserem Nenner b×b vorkommen muss:
Dann bringt aber unser Nenner b×b eben auch gleich zweimal den Teiler 2 für den Ergebnisnenner mit:
Daraus ergibt sich insgesamt folgendes Bild:
Wir sehen, dass der Ausdruck „2×2” sowohl im Zähler als auch im Nenner unseres Ergebnisses vorkommt und sich daher quasi gegenseitig aufhebt, weil man ihn sofort wegkürzen kann:
Damit verschwinden aber insbesondere gleich auch wieder beide Zweien, die uns der Zähler a×a für den Ergebniszähler geliefert hat und wir stehen letztlich ganz ohne 2 im Zähler des Ergebnisses da, so dass niemals eine 2 aus (a×a)÷(b×b) hervorgehen kann.
Sicher, vielleicht ist ja noch in dem als „…” dargestellten Rest des Zählers eine 2 enthalten. Aber damit wären wir wieder bei der eben angestellten Überlegung angelangt, denn diese 2 müsste ja auch irgendwie aus a×a hervorgegangen sein, so dass sie – wie eben langatmig dargelegt – dann auch gleich wieder doppelt im Zähler vorkäme. Jeder Versuch, eine dieser beiden Zweien durch eine einzelne 2 im Nenner zu „neutralisieren” würde dann aber wieder – wie eben gezeigt – gleich beiden Zweien im Zähler auf einmal den Garaus machen. Mit anderen Worten: die 2, die aus (a×a)/(b×b) hervorgehen soll, würde immer im Doppelpack aus dem Zähler a×a hervorgehen und könnte andererseits nur im Doppelpack aus dem Nenner b×b heraus weggekürzt werden. Daher kann sie nie einzeln im Zähler des Ergebnisses auf der rechten Seite der Ausgangsgleichung erscheinen, so dass dort niemals 2 herauskommen kann.
Etwas anderes wäre es, wenn wir die Wurzel aus einer Zahl suchten, die selbst das Quadrat aus einer ganzen Zahl ist – sagen wir 9 (also 3×3). Dann muss die 9 nicht unbedingt selbst in a enthalten sein, damit a×a durch 9 teilbar ist, denn a könnte ja zweckmäßigerweise gerade 3 sein. In der Tat ist es so, dass jeder Bruch, dessen Zähler und Nenner jeweils Quadrate ganzer Zahlen sind, eine Wurzel hat, die selbst eine rationale Zahl ist. Für die allermeisten Brüche ist das aber halt leider nicht der Fall.
Also ob Euch das jetzt einen Erkenntnisgewinn verschafft hat oder nicht – bei mir ist der Groschen immerhin gefallen. Endlich habe ich mir eine klare Vorstellung davon erarbeitet, warum die Wurzel aus 2 nicht rational sein kann. War nett von Euch, dass Ihr mir dabei zugehört habt. Ehrlich. Danke!
Alles Liebe
Daniel












Sehr cool! Hier vielleicht noch eine etwas einfachere Betrachtungsweise des selben Prinzips. Angenommen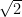 wäre rational, d.h.
wäre rational, d.h. 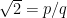 . Daraus folgt:
. Daraus folgt:  . Sowohl
. Sowohl  als auch
als auch  müssen als Quadrate eine gerade Anzahl von Primfaktoren (insbesondere vom Faktor 2) haben.
müssen als Quadrate eine gerade Anzahl von Primfaktoren (insbesondere vom Faktor 2) haben.  hat aber eine ungerade Anzahl an 2‑Faktoren. Widerspruch.
hat aber eine ungerade Anzahl an 2‑Faktoren. Widerspruch.
Megacool! Das ist wirklich der Beweis auf sein absolutes essentielles Minimum reduziert und perfekt auf den Punkt gebracht. Danke! Allerdings glaube ich, dass der nicht-mathematische Mensch mit dieser ebenso kompakten wie eleganten Beweisdarstellung etwas überfordert wäre. Insofern ist meine etwas längliche Umschreibung desselben möglicherweise aus didaktischer Sicht für nicht-mathematische Menschen adäquater.
Übrigens, wenn man Deine Version auf die Wurzeln von Zahlen ausweiten will, die selbst keine Primzahlen sind — also etwa die 6 — dann muss man auf die Anzahl der Vorkommen jedes einzelnen Primfaktors abstellen, denn am Beispiel 6 mit den Primfaktoren 2 und 3 käme sonst durchaus insgesamt eine gerade Anzahl an Primfaktoren für heraus.
heraus.
Du hast natürlich recht mit den einzelnen Primfaktoren. So habe ich es auch gemeint. Allerdings ist für den Beweis tatsächlich nur die Anzahl des Primfaktors 2 relevant.